What is Seasonality?
우리는 시계열의 평균에 규칙적이고 주기적인 변화가 있을 때마다 시계열은 Seasonality을 나타낸다고 말합니다. Seasonality 변화는 일반적으로 시계와 달력을 따릅니다. 하루, 일주일 또는 1년에 걸쳐 반복되는 것은 일반적입니다. Seasonality은 종종 일 년 또는 날짜와 시간을 둘러싼 사회적 행동의 규칙에 의해 결정됩니다.
우리는 계절성을 모델링하는 두 가지 종류의 특징을 배울 것입니다. 첫 번째 종류인 지표는 일별 관측치의 주 시즌과 같이 관측치가 적은 계절에 가장 적합합니다. 두 번째 종류인 푸리에 특징은 일별 관측치의 주 시즌과 같이 관측치가 많은 계절에 가장 적합합니다.
Seasonal Plots and Seasonal Indicators
이동 평균 그림을 사용하여 일련의 추세를 발견한 것과 마찬가지로 계절 그림을 사용하여 계절 패턴을 발견할 수 있습니다.
Seasonal indicators
계절 지표는 시계열 수준의 계절적 차이를 나타내는 이항적 특징입니다. 계절 지표는 계절 기간을 범주형 특징으로 취급하고 원-핫 인코딩을 적용하면 얻을 수 있는 것입니다.
일주일 중 한 번의 핫 인코딩 데이를 통해 주간 계절 지표를 얻을 수 있습니다. 그러면 삼각법 시리즈에 대한 주간 지표를 만들면 6개의 새로운 "더미" 기능을 얻을 수 있습니다. (선형 회귀 분석은 지표 중 하나를 떨어뜨리면 가장 효과적입니다. 아래 프레임에서 월요일을 선택했습니다.) -> 월요일이 0 인 이유

훈련 데이터에 계절 지표를 추가하면 모델이 계절 기간 내의 평균을 구별하는 데 도움이 됩니다:

표시기는 On/Off 스위치 역할을 합니다. 언제든지, 이 표시기들 중 최대 하나는 1(On)의 값을 가질 수 있습니다. 선형 회귀 분석은 Mon에 대한 기준 값 2379를 학습한 다음 해당 날짜에 On인 표시기의 값으로 조정합니다. 나머지는 0이고 사라집니다.
Fourier Features and the Periodogram
지표가 비실용적인 많은 관측치보다 긴 계절에 더 적합한 것은 지금 논의하는 특징의 종류입니다. 푸리에 특징은 각 날짜에 맞는 특징을 만드는 대신 몇 가지 특징만으로 계절 곡선의 전체적인 모양을 포착하려고 합니다.
우리가 푸리에 함수로 포착하려고 시도하는 것이 바로 계절 내의 이러한 진동수입니다. 이 아이디어는 우리가 모델링하려는 계절과 동일한 진동수를 갖는 주기 곡선을 훈련 데이터에 포함시키는 것입니다. 우리가 사용하는 곡선은 삼각함수인 사인과 코사인의 곡선입니다.
푸리에 특징은 사인 곡선과 코사인 곡선의 쌍으로, 가장 긴 것으로 시작하는 계절의 잠재적 빈도마다 한 쌍씩입니다. 연간 계절성을 모델링하는 푸리에 쌍에는 빈도가 연간 1회, 연간 2회, 연간 3회 등이 있을 것입니다.
이 사인/코사인 곡선의 집합을 훈련 데이터에 추가하면 선형 회귀 알고리즘은 대상 시리즈에서 계절 성분에 맞는 가중치를 계산할 것입니다. 그림은 위키 삼각법 시리즈에서 선형 회귀가 연간 계절성을 모델링하기 위해 4개의 푸리에 쌍을 사용한 방법을 보여줍니다.
연간 계절성을 잘 추정하기 위해서는 8개의 특징(4개의 사인/코사인 쌍)만 필요했습니다. 이를 수백 개의 특징(1년 중 매일 하나씩)이 필요했던 계절 표시 방법과 비교해 보십시오. 푸리에 특징으로 계절성의 "주효과"만 모델링하면 일반적으로 훈련 데이터에 훨씬 적은 특징을 추가해야 하는데, 이는 계산 시간이 단축되고 과적합 위험이 적다는 것을 의미합니다.
Choosing Fourier features with the Periodogram
우리는 실제로 몇 개의 푸리에 쌍을 특징 집합에 포함시켜야 할까요? 우리는 이 질문에 주기도식으로 답할 수 있습니다. 주기도식은 시계열에서 진동수의 세기를 알려줍니다. 구체적으로 그래프의 y축에 있는 값은 (a ** 2 + b ** 2) / 2 이고, 여기서 a와 b는 그 진동수에서 사인과 코사인의 계수입니다.
Example - Tunnel Traffic
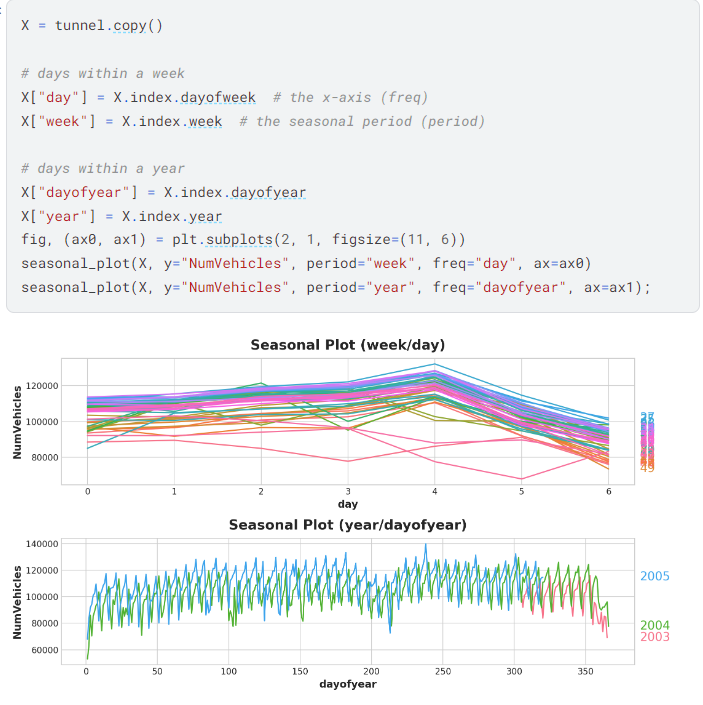
seasonal plots over a week and over a year
the periodogram
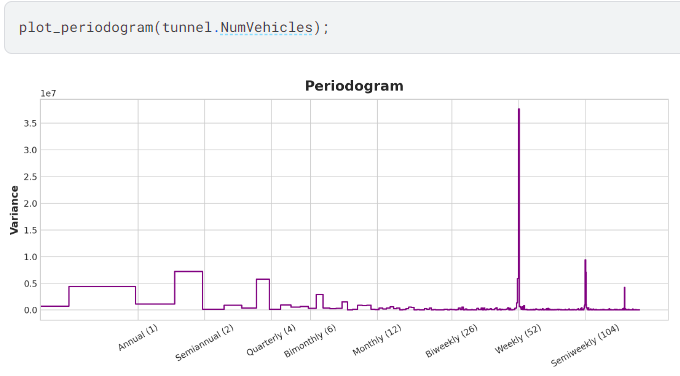
위의 계절 그림과 일치하는 것이 바로 강한 주간 계절과 약한 연간 계절입니다. 지표를 사용하여 모형을 만들 주간 계절과 푸리에 기능을 사용하여 연간 계절입니다. 오른쪽에서 왼쪽으로, 주기도는 격월(6)과 월간(12) 사이에 있으므로 10개의 푸리에 쌍을 사용해 보겠습니다.
우리는 2과에서 추세 특징을 만들기 위해 사용했던 것과 동일한 유틸리티인 결정론적 프로세스를 사용하여 계절 특징을 만들 것입니다. 두 계절 기간(주간 및 연간)을 사용하려면 그 중 하나를 "추가 용어"로 인스턴스화해야 합니다:

기능 집합을 생성하면 모델을 적합시키고 예측을 수행할 준비가 되어 있습니다. 우리는 90일 예측을 추가하여 우리 모델이 훈련 데이터 이상으로 어떻게 외삽하는지 확인할 것입니다. 여기서 코드는 이전 수업에서 사용한 코드와 동일합니다.
예측을 개선하기 위해 시계열로 할 수 있는 일은 훨씬 더 많습니다. 다음 시간에는 시계열 자체를 특징으로 사용하는 방법에 대해 배울 것입니다. 시계열을 예측의 입력으로 사용하면 직렬에서 종종 발견되는 또 다른 구성 요소인 사이클을 모델링할 수 있습니다.
'Kaggle Learn' 카테고리의 다른 글
| Time Series as Features (0) | 2024.05.22 |
|---|---|
| Time Series - Trend (0) | 2024.05.21 |
| Time Series - Linear Regression With Time Series (1) | 2024.05.21 |
| Data Visualization - Choosing Plot Types and Custom Styles (0) | 2024.03.23 |
| Data Visualization - Distributions (0) | 2024.03.23 |



